Il gioco delle targhe
Ormai non si vedono più in giro le vecchie targhe con sei cifre, sostituite da quelle nuove con quattro lettere e tre numeri.
Per questo, ogni volta che ne vedo una vecchia, sono particolarmente soddisfatto e non posso fare a meno di "divertirmi" a risolvere il giochino matematico che ora vi spiego.
Si tratta di inserire tra le cifre della targa i segni matematici necessari (parentesi incluse) per fare in modo che l'operazione ottenuta dia come risultato 0. Qualche esempio può aiutare a chiarire meglio cosa intendo.

[(1 + 8) - 9] x 484

(1 x 6) - (3 x 2) x 36
Talvolta una delle possibili soluzioni richiede l'impiego di segni matematici meno classici, quali la radice quadrata o il segno di esponente (^).
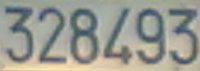
3284 x [radice_quadrata(9) - 3]

5 x [(9 - 7 + 1)^2 - 9]
Comunque la cosa bella è che ogni vecchia targa mi propone un nuovo gioco. Talvolta la proposta è tanto facile da essere banale, come quando la targa contiene zeri o due cifre uguali una accanto all'altra: in questi casi è facile, una volta ottenuto lo zero, moltiplicarlo per ciò che lo precede e per ciò che lo segue, ottenendo evidentemente zero.
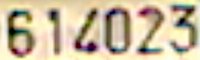 In questo caso infatti è semplice "risolvere" la targa in questo modo: 614 x 0 x 23
In questo caso infatti è semplice "risolvere" la targa in questo modo: 614 x 0 x 23
Si può comunque provare a "salvare" la targa rimuovendo lo zero e utilizzando la cinquina di numeri rimanente: in questo caso resterebbe 61423 risolvibile in parecchi modi tra cui (6 x 1 - 4 - 2 ) x 3 oppure 61 x (radice_quadrata(4) - 2) x 3.
Talvolta invece il gioco che ne vien fuori è assai più difficile e richiede un certo impegno x essere risolto ma una soluzione esiste sempre. O quasi sempre? Questo sì che sarebbe un compito da veri matematici, ovvero dimostrare che tutte le possibili targhe (ovvero novecentonovantanovemilanovecentonovantanove, tutti i numeri da 000001 a 999999) possono essere "risolti" secondo il mio gioco.
Ovviamente quasi tutte le targhe hanno molteplici soluzioni, come mostrano questi esempi.

(59 - 57) x 4 - 8
5 + 9 + 5 - 7 - 4 -8
(5 + 9) x (5 + 7 - 4 - 8)
(5 + 9 - 5 - 7) x 4 - 8
E ora, provate a ricordarvi la targa della macchina che tanti anni fa avevate voi o i vostri genitori: riuscite a "risolverle"? Scrivete nei commenti alcune targhe che siete riusciti ad "azzerare" oppure altre che vi stanno proprio facendo impazzire... magari la soluzione è più ovvia di quanto vi sembri! :)
Sennò provate a risolvere questo semplice esempio... vediamo chi sarà il primo a scrivere la soluzione come commento! Io ho trovato 4 modi per risolvere questa targa, vediamo quanti ne trovate voi!
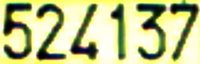
5 x (-2 + 4) x 1 - (3 + 7)
52 x (4 - 1 - 3) x 7
5 x [- 2 + (4 - 1) ^ 3 - 7]
52 x (4 x 1 + 3 - 7)
Per potervi "divertire" un po', potete usare questo generatore di targhe che ho realizzato (e che, per non farvi perdere tempo, evita di proporvi le targhe che includono zeri)! :)
P.S.: perché ho come l'impressione che, dopo questa digressione matematica sul mio blog, il numero dei miei lettori diminuirà drasticamente? :-p
Per questo, ogni volta che ne vedo una vecchia, sono particolarmente soddisfatto e non posso fare a meno di "divertirmi" a risolvere il giochino matematico che ora vi spiego.
Si tratta di inserire tra le cifre della targa i segni matematici necessari (parentesi incluse) per fare in modo che l'operazione ottenuta dia come risultato 0. Qualche esempio può aiutare a chiarire meglio cosa intendo.


Talvolta una delle possibili soluzioni richiede l'impiego di segni matematici meno classici, quali la radice quadrata o il segno di esponente (^).
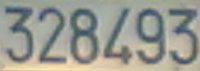

Comunque la cosa bella è che ogni vecchia targa mi propone un nuovo gioco. Talvolta la proposta è tanto facile da essere banale, come quando la targa contiene zeri o due cifre uguali una accanto all'altra: in questi casi è facile, una volta ottenuto lo zero, moltiplicarlo per ciò che lo precede e per ciò che lo segue, ottenendo evidentemente zero.
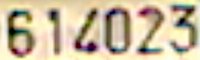 In questo caso infatti è semplice "risolvere" la targa in questo modo: 614 x 0 x 23
In questo caso infatti è semplice "risolvere" la targa in questo modo: 614 x 0 x 23Si può comunque provare a "salvare" la targa rimuovendo lo zero e utilizzando la cinquina di numeri rimanente: in questo caso resterebbe 61423 risolvibile in parecchi modi tra cui (6 x 1 - 4 - 2 ) x 3 oppure 61 x (radice_quadrata(4) - 2) x 3.
Talvolta invece il gioco che ne vien fuori è assai più difficile e richiede un certo impegno x essere risolto ma una soluzione esiste sempre. O quasi sempre? Questo sì che sarebbe un compito da veri matematici, ovvero dimostrare che tutte le possibili targhe (ovvero novecentonovantanovemilanovecentonovantanove, tutti i numeri da 000001 a 999999) possono essere "risolti" secondo il mio gioco.
Ovviamente quasi tutte le targhe hanno molteplici soluzioni, come mostrano questi esempi.

5 + 9 + 5 - 7 - 4 -8
(5 + 9) x (5 + 7 - 4 - 8)
(5 + 9 - 5 - 7) x 4 - 8
E ora, provate a ricordarvi la targa della macchina che tanti anni fa avevate voi o i vostri genitori: riuscite a "risolverle"? Scrivete nei commenti alcune targhe che siete riusciti ad "azzerare" oppure altre che vi stanno proprio facendo impazzire... magari la soluzione è più ovvia di quanto vi sembri! :)
Sennò provate a risolvere questo semplice esempio... vediamo chi sarà il primo a scrivere la soluzione come commento! Io ho trovato 4 modi per risolvere questa targa, vediamo quanti ne trovate voi!
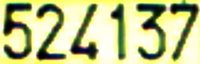
52 x (4 - 1 - 3) x 7
5 x [- 2 + (4 - 1) ^ 3 - 7]
52 x (4 x 1 + 3 - 7)
Per potervi "divertire" un po', potete usare questo generatore di targhe che ho realizzato (e che, per non farvi perdere tempo, evita di proporvi le targhe che includono zeri)! :)
P.S.: perché ho come l'impressione che, dopo questa digressione matematica sul mio blog, il numero dei miei lettori diminuirà drasticamente? :-p




E' giusto 5+2+4-1-3-7 o è una castroneria matematica?
(5-2-4+1)*37
Giusto, ma ci sono anche tanti altri modi... su, datevi da fare! :)
Ovviamente sono giusti entrambi i modi, sia quello di Anonimo sia quello di Tommi!
Oh mio dio O_O
Ed io che mi preoccupo dei miei discorsi col bambù che ho in camera (prima li facevo col gatto che ammetto dava più soddisfazione...ma ora sta dai miei...) ma vedo che anche qui c'è chi non è messo proprio bene, eh XD
5^2-(4*1+3*7)
scusa Fra,ma nella tua terza soluzine con (4-1)^3 intendevi * "per"?? perchè io con "^" intendo "elevato" ma non tornerebbe...
Hai perfettamente ragione Giuly, mi sono sbagliato! :)
Grazie per la correzione
Uno ci ha provato senza troppa convinzione, ma io mi chiedo lo stesso perchè non sei stato coperto di insulti...
detto questo: la mia vecchia clio era Ca670602 ma con due zeri è troppo facile vero? quindi li tolgo secondo il tuo prncipio e resta 6762 ...ehm io conosco solo due o tre addizioni e un paio di sottrazioni... riesci a risolvermelo tu?
Mi dispiace ma ho proprio paura che togliendo gli zeri non sia risolvibile! :(
Se qualcuno ci dovesse riuscire gli offro una pizza!
Io ne ho una un po' contorta, spero che vada bene cmq:
il numero è 6762, no?
Allora: (log(in base 6) di (7-6))*2 = (log (in base 6) di 1))*2 = 0 * 2 = 0
in quanto il logaritmo, in qualunque base, di 1 è uguale a 0.
Aspetto la pizza!!
Sarò sincero... io cercavo di risolvere tutte le targhe usando solo simboli matematici grafici e cioè (, ), +, -, *, /, ^ e radice_quadrata.
Mi resta ancora il dubbio se considerare tale anche il logaritmo (che poi andrebbe bene anche il logaritmo naturale, non serve che sia in base 6, la targa infatti può essere risolta così: 6*ln(7-6)*2 = 0).
La tua soluzione comunque è talmente originale che la pizza te la sei meritata tutta comunque... appena ci vediamo sarà tua! :)